|
|
|
| ||
|
Superfluid helium as a vacuum What is the minimum number of atoms needed for superfluidity?
According to the results of a remarkable molecular spectroscopy
experiment, there is definite proof that a system of only 60 atoms can be
superfluid. Slava Grebenev and colleagues at the Max Planck Institute for Fluid
Dynamics in Göttingen, Germany, found that small molecules dissolved
in droplets of liquid helium can rotate freely, just like they do in a
vacuum (S Grebenev, J P Toennies and A Vilesov 1998 Science
279 2083). The molecules rotate freely because the surrounding
helium is a "superfluid" - a liquid without viscosity. In effect, the
liquid helium acts as a vacuum.
In an ingenious series of experiments the Göttingen team squirted liquid helium through a fine nozzle to create drops containing about 104 atoms at a temperature of 0.1 K. The team used laser spectroscopy to probe the rotational behaviour of oxygen carbon sulphide (OCS) molecules that had been dissolved in the helium. The experiment was set up so that there was just one OCS molecule in each droplet. Even though the OCS molecule was in the middle of the liquid helium, the researchers found that its rotational spectra was the same as that of a molecule in free space except that the moment of inertia appeared to be 2.7 times larger. This factor is due to the additional mass of a helium coating on the surface of the OCS molecule. The crucial contribution of the Göttingen group was to show that the molecule was not on the surface of the drop and that superfluidity - rather than some other property of the droplets - was definitely responsible for the behaviour. To understand the significance of the superfluidity recall that helium has two stable isotopes. Both isotopes experience very weak attractive forces, but they differ in mass and, more importantly, quantum statistics. The naturally occurring isotope, helium-4, is a boson. As a consequence, below a temperature of about 2 K it "Bose condenses" into an unusual state in which many of the atoms are in the same quantum state. In this state the helium is superfluid and loses all viscosity. The other isotope, helium-3, is very rare in nature, although it is an important by-product of nuclear weapons production. Helium-3 is a fermion, so the atoms in the liquid must occupy different quantum states. This means that helium-3 becomes superfluid at a much lower temperature, about 3 mK - a discovery recognized by the award of the Nobel Prize for Physics to Lee, Osheroff and Richardson in 1996. When the Göttingen group first performed experiments on an impurity molecule inside helium-3 droplets they found, to their surprise, that free rotation was still evident, even though the droplet had not been cooled below the superfluid transition temperature of helium-3. They soon realized, however, that a very small concentration of helium-4 atoms in a helium-3 droplet could be enough to allow the molecule to rotate. The helium-4 atoms are attracted to the molecular impurity because they are heavier and form a superfluid around it. When the team used ultra-pure helium-3 they found that non-superfluid helium acted like a viscous liquid and damped out molecular rotations. Then they did something very interesting. They added helium-4 in measured amounts, coating the OCS molecule with a few helium-4 atoms at a time. Free rotation was restored when about 60 atoms of helium-4 surrounded the OCS molecule.
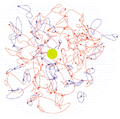
The physics of the superfluid drop is easy to understand and calculate using the path integral technique introduced by Richard Feynman in 1953. In this method, a helium-4 atom is represented by a loop of string; the colder the temperature, the longer the loop. Because helium-4 atoms are indistinguishable bosons, two or more loops can join together to form "super-loops". Feynman explained that the superfluid state is an entangled liquid of these loops, with many loops extending right across the sample (see figure). The entanglement gives rise to the different dynamical properties. When the helium-4 forms an entangled liquid, most of the excited quantum states disappear because, otherwise, all of the entangled atoms would have to simultaneously make a transition to the excited state. This leads to an "energy gap" between the ground state and the excited states. If the impurity molecule absorbs a photon from the laser and rotates, the surrounding superfluid will respond without exchanging momentum and energy with the molecule. The only effect is that some helium-4 atoms rotate as a rigid body with the molecule. On the other hand, a normal liquid, even a very quantum one like helium-3, has many accessible states. Therefore, when the molecule begins to rotate, some of the surrounding atoms are excited to higher quantum states and travel out to the surface of the atom, where they evaporate. This means that the OCS molecule soon comes to rest. Why are 60 atoms needed to see this effect? Clearly one has to surround the molecule with a full layer of helium-4 atoms (about 20 atoms) to insulate it from the liquid helium-3. Also, the helium-4 atoms immediately adjacent to the OCS molecule are localized by the strong chemical forces and rotate with the molecule. Hence about two layers or 40-60 helium-4 atoms are needed. The superfluid state is often defined as having the property of "off-diagonal long-range order". This means that its quantum phase maintains a constant value over long distances. This is an unnecessarily narrow definition because it denies the possibility of superfluidity in a finite system like the helium-4 droplet. An analogy to a crystal will help the reader to understand this issue. Textbooks define a crystal as an infinite number of atoms precisely lined up. With this definition, however, we cannot speak of a "microcrystal" of say 200 atoms. But in practice it is clearly possible to differentiate between a "microcrystal" and a "microliquid", primarily based on their different dynamical properties. The best definition of superfluidity, originally given by Lev Landau in 1941, is precisely what is measured in the Göttingen experiment: the response of the fluid to the motion of an impurity. This definition works for very small systems. What is fascinating about this new experiment is the juxtaposition of chemistry with superfluidity. On the one hand, it is a new environment for studying molecules. There has been speculation that molecules that are unstable in a "real" vacuum might be stable in the helium-4 "vacuum". On the other hand, the molecules can probe for superfluidity. For example, an open question is whether vortices can exist in these small droplets. It should also be possible to test theoretical predictions about hydrodynamical coupling between rotations in liquids by placing two molecules in a droplet. Author
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Home | News | Physics World | PhysicsJobs | Resources | Events | Best of PhysicsWeb Tel +44 (0)117 929 7481 | Fax +44 (0)117 925 1942 | E-mail info@physicsweb.org | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||